Anamorphisms in JavaScript

preamble: unfolds and folds

Anamorphisms are functions that map from some object to a more complex structure containing the type of the object. For example, mapping from an integer to a list of integers.

Here’s an anamorphism:

function downToOne(n) {
  const list = [];

  for (let i = n; i > 0; --i) {
    list.push(i);
  }

  return list;
}

downToOne(5)
  //=> [ 5, 4, 3, 2, 1 ]

An integer is our object, and the array containing integers is our “structure containing integers.” Maps from integers to arrays of integers are anamorphisms. “Anamorphism” is a very long word, and using it implies that we are going to be strict about following category theory. So let’s use a simpler word that has some poetic value: Unfold. Anamorphisms “unfold” values into more complex structures containing those values.

I like to think of the integer 5 as having all the whole numbers less than five folded up inside itself.

So we’ll use the word “unfold” from now on.

Unfolds (or anamorphisms) are the dual—a fancy word for complement—of Catamorphisms, functions that map from some complex structure containing values down to values.

Here’s a catamorphism:

function product(list) {
  let product = 1;

  for (const n of list) {
    product *= n;
  }

  return product;
}

product(downToOne(5))
  //=> 120

“Catamorphism” is another long word that implies that we are going to be strict about following category theory. So let’s call these things folds instead. We can think of product as folding a list of integers into an integer.

folding and unfolding with generators

Unfolding a number into a list is questionable practice. It takes up a lot of space, and we just want to iterate over it, as we did above with product. Well, we can unfold it into a finite iteration with a generator:

function * downToOne(n) {
  for (let i = n; i > 0; --i) {
    yield i;
  }
}

[...downToOne(5)]
  //=> [ 1, 2, 3, 4, 5 ]

Remember our product definition? Thanks to the way a for... of loop works in JavaScript, it folds any iterable of integers:

function product(iterable) {
  let product = 1;

  for (const n of iterable) {
    product *= n;
  }

  return product;
}

product(downToOne(5))
  //=> 120

Folding and unfolding work very well with iterators.

generalizing folds

We know that there is a very handy way to fold arrays, we can use the .reduce method:

function product(list) {
  return list.reduce((acc, n) => acc * n, 1);
}

product(downToOne(5))
  //=> 120

const factorial = (n) => product(downToOne(n));

The two problems we have with .reduce are that first, it takes multiple arguments, and second, it is a method on arrays and not on everything iterable. But it’s a useful pattern, and we can reproduce it by hand.

Here we create a foldWithFnAndSeed function that takes a folding function and a seed value, and gives us back a fold function. We use that to make our own product fold:

function foldWithFnAndSeed(fn, seed) {
  return function fold (iterable) {
    let acc = seed;

    for (const element of iterable) {
      acc = fn(acc, element);
    }

    return acc;
  }
}

const product = foldWithFnAndSeed(
    (acc, n) => acc * n, 1
  );

product(downToOne(5))

A variation uses the first element of the iterable as the seed, then iterates over the remainder. This is adequate for many purposes, including product:

function foldWith(fn) {
  return function fold (iterable) {
    const iterator = iterable[Symbol.iterator]();
    let { value: acc } = iterator.next();

    for (const element of iterator) {
      acc = fn(acc, element);
    }

    return acc;
  }
}

const product = foldWith(
    (acc, n) => acc * n
  );

product(downToOne(5))

For historical reasons, reduce in JavaScript takes two positional arguments, and we have to remember what they are and what order they’re in. Those reasons no longer exist: JavaScript, like nearly every other language in this century, has rediscovered what Smalltalk knew in 1980: named parameters are better. So we’ll use destructuring to emulate named parameters:

function foldWith(fn) {
  return function fold (iterable) {
    const iterator = iterable[Symbol.iterator]();
    let { value: acc } = iterator.next();

    for (const element of iterator) {
      acc = fn({ acc, element });
    }

    return acc;
  }
}

const product = foldWith(
    ({ acc, element: n }) => acc * n
  );

product(downToOne(5))

generalizing unfolds

Our foldWith function is handy, and we can use the same general idea for making unfolders. We want to end up with an unfoldWith function that takes, as its argument, a function for unfolding elements.

What will this function look like? The opposite of the function we used to fold, in that it will take a value as its argument, and return the next value, an element to yield, and whether it is done. Naturally, we’ll use destructuring to extract multiple return values:

function unfoldWith(fn) {
  return function * unfold (value) {
    let { next, element, done } = fn(value);

    while (!done) {
      yield element;
      ({ next, element, done } = fn(next));
    }
  }
}

const downToOne = unfoldWith(
    (n) => n > 0
    ? {
        element: n,
        next: n - 1
      }
    : { done: true }
  );

product(downToOne(5))
  //=> 120

For a moment, let’s close our eyes very tightly, plug our ears with our fingers, and murmur “la-la-la-la-la” at the thought of performance costs or implementation limits. Ready? Ok:

If we didn’t have a looping construct like while, we could write unfoldWith recursively:

function unfoldWith(fn) {
  return function * unfold (value) {
    let { next, element, done } = fn(value);

    if (!done) {
      yield element;
      yield * unfold(next);
    }
  }
}

const downToOne = unfoldWith(
    (n) => n > 0
      ? {
          element: n,
          next: n - 1
        }
      : { done: true }
  );

product(downToOne(5))
  //=> 120

It works just the same up until JavaScript’s stack overflows.

Reminder: yield * yields all the elements of an iterable, so yield * unfold(next) will yield the remaining elements.

Although it may be impractical for working at scale, what is interesting about the recursive unfold is that it encodes very directly how to do an unfold using linear recursion: Given a structure, turn it into part of the result and a structure representing the rest of the work to do.

In the case of unfolding, we take a structure, and return an element and a structure representing the part we haven’t unfolded yet. We then yield the element and the result of unfolding the rest of the structure.

Divide-and-conquer algorithms all have this structure: Break the problem into parts, apply the algorithm to each part, then glue the results back together. Recursive divide-and-conquer applies the exact same algorithm at finer and finer scale until a simple case is reached.

Linear recursion is a special case of divide-and-conquer, where we break the simple case off, solve it, and recursively apply our algorithm to the remainder of the input.

traversing lists, trees and forests

A traversal, or path, is a function that takes a structure and returns its elements as an iterator. JavaScript gives us built-in traversals for returning the values in arrays, we just iterate over them. But sometimes we want to iterate in another order. For that, we need a traversal.

One handy use for unfolds is to use them to express traversals. We can do that with an array. Here’s one that uses our unfoldWith exactly as described: it divides a non-empty array into an element and the rest of the array to unfold:

const butLast = (array) => array.slice(0, array.length - 1);
const last = (array) => array[array.length - 1];

const inReverse = unfoldWith(
    (array) => array.length > 0
      ? {
          element: last(array),
          next: butLast(array)
        }
      : { done: true }
  );

[...inReverse(['a', 'b', 'c'])]
  //=> ['c', 'b', 'a']

This is simple, but it makes successive copies of the array, and in JavaScript, this is expensive. It would be easier if we used the original array, but managed a cursor to keep track of our position in the array.

function * inReverse(array, cursor = array.length - 1) {
  if (cursor >= 0) {
    yield array[cursor];
    yield * inReverse(array, cursor - 1);
  }
}

[...inReverse(['a', 'b', 'c'])]
  //=> ['c', 'b', 'a']

We can easily write this with a while loop, but there is more interesting business afoot.

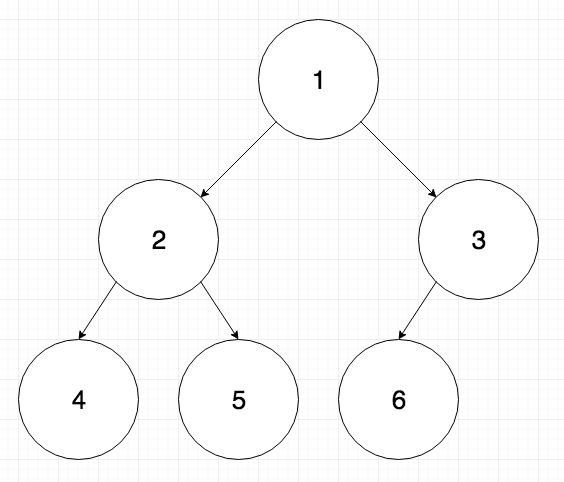
Consider this binary tree:

Image © Sam Gavis-Hughson, Coding Interview Question: Balanced Binary Tree

This tree can be represented as a nested POJO:

const tree = {
    label: 1,
    children: [
      {
        label: 2,
        children: [
          {
            label: 4,
            children: []
          },
          {
            label: 5,
            children: []
          }
        ]
      },
      {
        label: 3,
        children: [
          {
            label: 6,
            children: []
          }
        ]
      }
    ]
  };

Let’s write a traversal for it:

function * elements (tree) {
  yield tree.label;
  for (const child of tree.children) {
    yield * elements(child);
  }
}

[...elements(tree)]
  //=> [ 1, 2, 4, 5, 3, 6]

Note that the form of this traversal is almost identical to the form of our recursive linear unfold. The big difference is that we start with one element, but the “remainder” of our work is multiple elements.

We can unify them. A tree is a divergent graph with a single root node. If we have a collection of root nodes, it’s called a forest. The second-simplest possible forest is a collection with just root, and that’s just like a tree.

So if we write a traversal for forests, we also get one for trees. We’ll give this a more descriptive name:

function * depthFirst (forest) {
  if (forest.length > 0) {
    const [first, ...butFirst] = forest;

    yield first.label;
    yield * depthFirst(first.children.concat(butFirst))
  }
}

const simpleForest = [tree];

[...depthFirst(simpleForest)]
  //=> [ 1, 2, 4, 5, 3, 6]

This looks more familiar! We can express this as a linear recursion unfold:

const first = (array) => array[0];
const butFirst = (array) => array.slice(1);

const depthFirst = unfoldWith(
    (forest) => forest.length > 0
      ? {
          element: first(forest).label,
          next: first(forest).children.concat(butFirst(forest))
        }
      : { done: true }
  );

[...depthFirst(simpleForest)]
  //=> [ 1, 2, 4, 5, 3, 6]

All this work brings us to this: Just as we can express forward and backwards traverses through a list, we can express different kinds of traversals through more complex structures, like trees or forests.

Here is a breadth-first traversal of a forest:

const breadthFirst = unfoldWith(
    (forest) => forest.length > 0
      ? {
          element: first(forest).label,
          next: butFirst(forest).concat(first(forest).children)
        }
      : { done: true }
  );

[...breadthFirst(simpleForest)]
  //=> [ 1, 2, 3, 4, 5, 6 ]

Notice how it looks almost exactly identical to the depth-first expression. This tells us that we have exploited the symmetry between the various paths we can take through a forest. A right-to-left breadth-first search is likewise easy to code:

const rightToLeftBreadthFirst = unfoldWith(
    (forest) => forest.length > 0
      ? {
          element: last(forest).label,
          next: last(forest).children.concat(butLast(forest))
        }
      : { done: true }
  );

[...rightToLeftBreadthFirst(simpleForest)]
  //=> [ 1, 3, 2, 6, 5, 4 ]

Writing traversals illustrates that not only can we can separate the way to iterate over a particular data structure from the things we do with its elements, but we can decompose the algorithm of traversing or unfolding such that we hide away questions like whether we are looping or recursing and focus on the traverse or unfold’s pertinent logic.

unfolds, wrapped up

When working with data structures, we often want to provide certain common operations on their elements. For example, questions like “What is the set of unique elements of this collection?” or “What is the sum of the numbers in this collection?”

If we write a traversal for the collection, we turn it into an iterator, and we can write a single generic fold over the resulting iteration. We can write:

const sum = foldWith(
    ({ acc, element }) => acc + element
  );

And it works with forests as easily as it works with lists:

sum([1, 2, 3, 4, 5, 6])
  //=> 21

sum(depthFirst(simpleForest))
  //=> 21

Writing traversals separates the concern of how to iterate over a data structure from the concern of what to do with the elements of the data structure.

You often hear the advice to write code in small functions, to avoid putting too many lines in one method. Obviously, we can break big methods up by extracting “helper” methods, and that will satisfy JSLint, but that is treating the symptom and not the problem.

Building blocks like unfoldWith serve to illustrate the idea that many algorithms do share common concerns. All we need to do is train ourselves to see the underlying symmetry between them, and we can decompose our functions and recompose them with abandon.

have your say

Have an observation? Spot an error? You can open an issue, discuss this on reddit, or even edit this post yourself!

RAGANWALD.COM